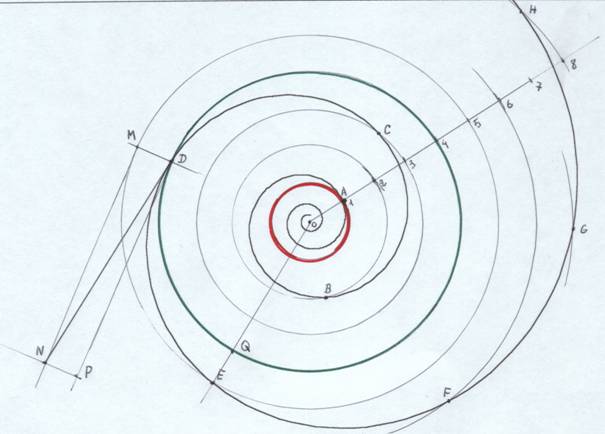
Je considère un univers fini, fermé, sans frontière, à une dimension, en expansion. Ce sera le cercle en expansion. Mon cercle aura un centre fixe, et son rayon, comme son périmètre, grandira régulièrement. Soit V la vitesse d'accroissement du périmètre.. Un point fixe A sur le cercle, soumis à la seule expansion, se déplacera suivant la direction d'un rayon. Un point S se déplacera sur le cercle, à partir de A, à la même vitesse V que grandit le périmètre. On pourra figurer ce mouvement sur une série de cercles concentriques, régulièrement espacés par une unité de temps.
L'unité est le cm. La spirale a été obtenue par l'ordinateur, sur la base des deux mouvements : 1 - Vitesse d'accroissement des rayons : 1 cm par unité de temps ; cela donne un accroissement du périmètre du cercle de 2π cm par unité de temps. 2 - Vitesse de déplacement d'un point S sur le cercle en expansion : 2π cm par unité de temps. Il y a donc correspondance entre la vitesse du mobile S sur le cercle et la vitesse d'accroissement du périmètre du cercle. Cette vitesse est celle du périmètre du cercle rouge par unité de temps. Le premier cercle rouge a un rayon de 1 cm, et un périmètre de 2π cm, les autres des rayons de 2, 3, 4...cm, et des périmètres de 4π, 6π, 8π cm, etc. La spirale est telle qu'elle coupe les cercles concentriques sous un angle constant. Cela entraîne que la spirale ne contient pas le centre des cercles. Elle se poursuit indéfiniment vers l'intérieur, se rapprochant du centre sans jamais l'atteindre. Ce fait correspondra, dans la suite de mon travail, à la singularité du big-bang.
Les portions successives de spirale, AB, BC, CD, etc. ont même longueur. Quelle est cette longueur ? Je raisonne ainsi pour la calculer : au point d'intersection D de la spirale avec un cercle, le mouvement de la spirale est soumis à deux vitesses, celle de 1 cm/s dans le sens du rayon, (vitesse centrifuge) celle de 2π/s dans le sens de la tangente au cercle. La résultante est DN, où nous avons DN2 = DM2 + DP2 Soit DN = racine de (1 +(2π)2).
Remarquons que si l'on poursuit le dessin de la spirale à l'infini, la figure courbe DMEQ finit par se confondre avec le rectangle DMNP. De même si, au lieu du cm, on choisit une unité de longueur extrêmement petite. La portion de spirale DE mesure racine de (1+4π2 ), soit 6, 362 cm au lieu de 6,283 cm pour 2π. La différence est la conséquence de l'expansion des cercles. Un raisonnement analogue nous permet de calculer la longueur limite de la partie de la spirale intérieure au premier cercle. C'est aussi Racine carrée de (1+(2π)2).
On peut calculer la valeur de l'angle de la spirale et des cercles. La tangente trigonométrique de l'angle NDP est 1 sur 2π soit 0,159. L'angle constant de la spirale et du cercle est de 9 degrés 4 centièmes. Je n'accorde pas grande importance à ce chiffre. Pour l'instant.
Le Dictionnaire des Sciences dit de cette spirale qu'elle est transcendante, logarithmique. Ajoutons-nous l'adjectif "fractal" ? Elle n'a pas d'équation. Pierre Odru (voir Annexe) note pourtant une équation en coordonnées polaires : R = exponentielle ((V/C) Phi), pour une vitesse d'expansion V, distincte de c. |