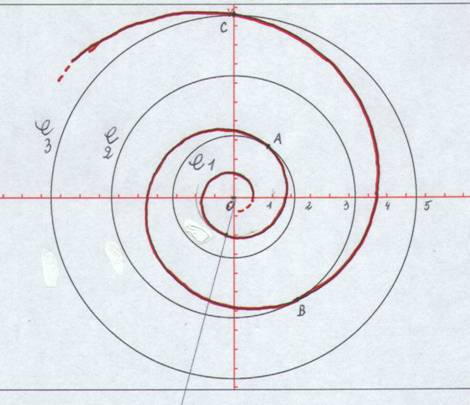
Il peut être intéressant d'étudier la même spirale en choisissant une autre unité de longueur. La spirale a été obtenue avec un logiciel de tracé mathématique, sur la base des deux mouvements :
1 - Sur le cercle : 1 (1dm/s) 2 - Suivant le rayon : 1/2π (0,159...dm/s)
Le cercle C1 a pour rayon 1 sur 2π dm, soit environ 0,159 dm, et pour périmètre 1 dm Le cercle C2 a pour rayon 2 sur 2π dm, soit environ 0,318 dm, et pour périmètre 2 dm Le cercle C3 a pour rayon 3 sur 2π dm, soit environ 0,477 dm, et pour périmètre 3 dm
Si l'on envisage le mouvement d'expansion du cercle C1 en C2, puis C3, de telle sorte que son périmètre s'accroîsse de 1 dm par seconde, et que le point A se déplace sur le cercle en expansion, à la vitesse de 1 dm par seconde, il parvient en B, puis en C, parcourant chaque fois, sur la spirale, une certaine longueur légèrement supérieure à 1 dm. Calculons-la, utilisant la fiche 6. La longueur de la portion de spirale et la distance parcourue par le point mobile sont dans le rapport racine de (4π2 plus1) et 2π. AB = BC = 6,362 divisé par 6,283 = 1,0126 dm Il en va de même pour la portion de spirale intérieure au premier cercle, qui tend vers une limite. Cette limite est 1,0126 dm. Je trouve remarquable de constater que le périmètre du premier cercle a sensiblement la même longueur que la spirale interne au premier cercle, qui tend vers une limite. Je dirai plus tard qu'il doit exister une quasi égalité entre le périmètre de notre Univers et le trajet de la lumière depuis l'origine, il y a quinze milliards d'années. L'expansion a donc entraîné, en même temps qu'un changement d'itinéraire, une vitesse légèrement supérieure. Cette augmentation intervient dans le fait que la lumière de l'origine nous parvient aujourd'hui, en ayant accompagné l'expansion.
La forme de la spirale est indépendante de l'échelle. Le cercle C 1 peut être la première seconde, le premier milliard d'années, etc.
Si l'on considère que le premier cercle dessiné représente l'Univers au premier milliard d'années, la partie intérieure de la spirale représente le premier milliard d'années-lumière en même temps que le périmètre du premier cercle est de un milliard d'années-lumière. Le temps équivaut à l'espace.
Si l'on dessine la spirale sur 15 cercles successifs, on aura la représentation du trajet de la lumière en 15 milliards d'années.
Ici, l'Univers en expansion est à une dimension plus le temps. Mais cet Univers à une dimension a la même métrique que l'Univers à deux dimensions (la surface de la sphère) et que l'Univers à trois dimensions, dans lequel nous vivons (espace courbe, impossible à se représenter).
NOTE Christian Magnan distingue entre un éloignement accompagné d'une vitesse et l'effet produit par l'expansion de l'Univers. Selon lui, cette dernière permettrait de concevoir une vitesse supérieure à celle de la lumière. Cette idée supprimerait la difficulté apparue à la fiche 4, où la vitesse de la lumière étant notée 2π, la vitesse sur la spirale atteindrait racine carrée de (4π2 + 1), soit 2π multiplié par 1,0126. Etudier le cercle en expansion sur la surface sphérique au repos, puis en expansion.
UN PROBLEME : la vitesse sur la spirale est plus grande que celle du périmètre du cercle. Si cette dernière est la vitesse de la lumière, alors un problème apparaît, car cette dernière est indépassable.de la lumière, pourtant indépassable Il existe une façon de résoudre ce problème. C'est de dessiner les cercles concentriques et la spirale sur une surface courbe.
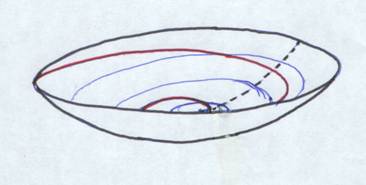
Je dessine ici une portion de surface courbe (peut-être parabolique), limitée par un cercle. Je dessine les cercles concentriques équidistants (distances mesurées sur le grand cercle pointillé). Dans quelles conditions aurons nous l'égalité entre la longueur de la spirale et le périmètre du cercle limite ? S'il s'agit d'une surface sphérique, la spirale reviendra sur elle même. C'est l'Univers fermé, qui reviendra sur Big creuch. S'il s'agit d'une paraboloïde ou d'une hyperboloïde, l'expansion continuera éternellement. Voir le cas d'une surface "gauche" (selle de cheval)
|