LES DIMENSIONS DE

L'ESPACE-TEMPS FERME

 

FICHE 6

 

Nous travaillerons sur l'univers fini, fermé, sans bord.

 

Une dimension : c'est, en particulier, le cercle. Un point s'y déplace dans les deux sens, on y mesure. Le cercle est un univers fermé, sans limite. Il n'a pas d'intérieur ou d'extérieur, ni de centre ou de rayon. Les points équidistants d'un point donné sont deux points du cercle de part et d'autre.

Ajoutons à cette première dimension le temps.

De l'un des points du cercle, on "voit" l'univers, à droite ou à gauche, sous forme d'un point qui n'a pas de dimension.

Si un point A de cet espace est en relation avec les autres points, il pourra apprécier leurs distances, en conclure que cet espace est en expansion. Si cette distance dépasse le demi-cercle, il pourra constater qu'un même point est visible plusieurs fois, dans les deux sens, que cet univers est fini.

 

LA REPRESENTATION DU TEMPS

 

 

Sur le cercle en expansion ci-contre, les points G, H, K, soumis à la seule expansion, sont figurés par des segments rayonnants.

Ex : G a existé du temps t 1 au temps t 3,5.

 

Si le point n'est pas immobile sur le cercle en expansion, son mouvement ne sera pas représenté par un segment de droite, mais par une ligne non droite. Ex : I

 

On conçoit aussi, sur une maquette, une représentation du mouvement dans le temps des points d'une surface sphérique soumise à l'expansion

 

 

 

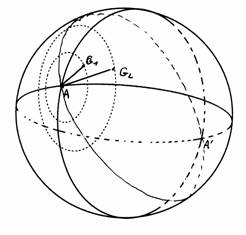
Deux dimensions : c'est la surface sphérique. D'un de ses points, on "voit" l'univers autour de soi, comme un nageur voit la surface de la mer, sous forme d'un cercle lorsqu'on se trouve à son centre.

Sur la surface sphérique, les points équidistants d'un point donné A forment un cercle de centre A, avec rayon incurvé.

A tout point A de la sphère correspondent:

Þ    Le point A', antipode de A ;

Þ    Un ensemble de tous les grands cercles contenant A et A' ; le dessin montre trois de ces grands cercles. Les demi-cercles en arrière de la figure sont en traits interrompus..

Þ    Un ensemble de cercles concentriques  déterminés par A et A' . Le dessin montre deux de ces cercles.

Pour toute paire de points P et P' de la sphère, on définit une distance PP' qui est la longueur de l'arc de grand cercle PP'.

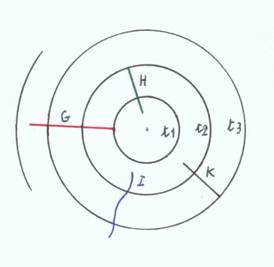
Trois dimensions : c'est l'espace qui nous est familier. On "voit" l'univers comme on voit l'intérieur d'une sphère lorsqu'on se trouve à son centre. C'est la "voûte" céleste.

Les points équidistants d'un point A donné forment une surface sphérique de centre A, au rayon certainement incurvé.

Dans cet univers plus le temps, on peut comprendre l'expansion de la surface sphérique de la deuxième dimension, et concevoir la forme (surface) obtenue en faisant pivoter autour de l'axe AO la spirale décrite par un mobile, et que je nomme "spiraloïde de révolution", dont nous allons parler?

 

On "voit" donc avec une dimension de moins que l'univers dans lequel on se considère.

On a remarqué que si le temps intervient dans la première dimension, il fait apparaître la deuxième (la spirale). De même que, pour la deuxième, il fait apparaître la spiraloïde (troisième).

La géométrie du cercle nous aide à comprendre celle de la surface sphérique. De même celle de la surface sphérique doit pouvoir nous aider à comprendre l'espace à trois dimensions, fini et courbe.

Ainsi H. Andrillat propose, en considérant ce qui se passe pour les cercles dessinés sur une sphère euclidienne, de l'extrapoler à des sphères se trouvant dans l'espace courbe. Considérons une sphère dont nous sommes au centre.

Si elle grandit suffisamment, elle atteindra une taille maximum, puis diminuera de taille, jusqu'à englober la totalité de l'Univers.

Les rayons de cette hyper-sphère seront courbes.

 

 

Léonard Mlodinov ( Dans l'œil du compas) Autre principe révolutionnaire établi par Gauss, c'était la possibilité d'étudier la courbure d'un espace uniquement à sa surface, sans référence à un espace plus vaste pouvant - ou non - le contenir. Plus techniquement, on peut étudier la géométrie d'une surface courbe sans référence à un espace euclidien de dimension supérieure. Que l'espace puisse « se courber » tout en ne se courbant dans rien était un concept qui allait s'avérer nécessaire à la théorie de la relativité générale ultérieurement élaborée par Einstein. Après tout, puisque nous ne pouvons pas nous glisser hors de notre univers pour contempler notre royaume tridimensionnel limité, il n'y a que ce genre de théorème qui nous donne l'espoir de pouvoir déterminer la courbure de notre propre espace.

 

 

Reste une difficulté : Le temps doit-il être considéré comme "la" quatrième dimension ? N'y a-t-il pas une quatrième dimension spatiale, que notre cerveau ne peut pas imaginer ? Le fait que l'origine de l'Univers est visible dans toutes les directions de l'espace semble le suggérer. Nous en reparlerons.