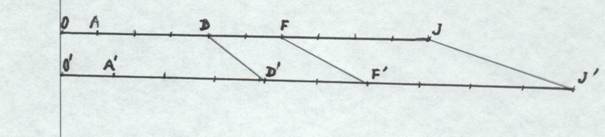
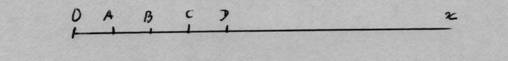L'élastique en expansion

Considérons un élastique OJ d'une longueur de 10 cm, où nous avons repèré les points séparés par 1 cm, avec OD=4, DF=2.

L'extrémité O étant fixe, tirons sur l'extrémité J, de façon que O'J' mesure 14 cm (10 multiplié par 1,4).

Nous avons O'D'=4 multiplié par 1,4= 5,6 cm, et D'F'= 2 multiplié par 1,4 = 2,8 cm.

Revenons à la position initiale, et faisons en sorte que J soit tiré à la vitesse de 4 cm/s.

D' se déplacera à la vitesse de 4 dixièmes de 4, soit 1,6 cm/s ; F' se déplacera à la vitesse de 6 dixièmes de 4, soit 2,4 cm/s, proportionnellement à leur place au départ sur l'élastique.

La distance DF s'accroîtra à la vitesse de 2 dixièmes de 4, soit à 0,8 cm/s.

Les vitesses d'éloignement de deux points sont proportionnelles à la distance qui les sépare.

La fourmi sur l'élastique en expansion

Tirons l'extrémité E vers la droite à une vitesse v et donnons aux mobiles la même vitesse v. O reste immobile, A se déplace à la vitesse de un dixième de v, D à la vitesse de 4 dixième de v, etc.

Considérons maintenant des points mobiles se déplaçant sur l'élastique, dans le même sens, comme le ferait une fourmi.

Le mobile partant de O aura au départ la vitesse v, mais qui augmentera régulièrement.

Le mobile partant de D aura au départ une vitesse de v plus 4 dixièmes de v, et cette vitesse augmentera en proportion de la place du mobile sur l'élastique.

Le mobile partant de I rattrapera le premier l'extrémité J, suivi par les autres, à des distances à calculer.

Voir fiche 4 un graphique de ces mouvements

La demi-droite en expansion

Considérons un élastique fixé à une extrémité O, gradué, et que l'on tire par l'autre extrémité. Les distances et les vitesses d'éloignement de deux points respectent la proportionnalité.

Si A et B s'éloignent l'un de l'autre à la vitesse de 1 cm/s, O et D s'éloigneront à la vitesse de 4 cm/s.

La droite en expansion

Un élastique que nous tirons par ses deux extrémités figurera une droite, illimitée dans les deux sens, en expansion.

Si au départ, la droite est graduée, les distances et les vitesses d'éloignement de deux points respecteront la proportionnalité.

Si OC ( 2 cm) grandit à la vitesse de 2 mm/s, le point X, qui est situé à 100 km à droite, s'éloignera de O à la vitesse de 10 km/s

Tout point de la droite pourra être considéré comme immobile, les autres points s'éloignant de lui.

Si l'instrument de mesure est soumis à l'expansion, comme la droite, l'expansion ne sera pas observable. Nous reviendront sur ce point à propos de l'expansion de l'Univers.

 Le plan en expansion

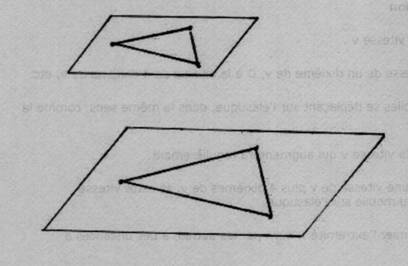
Homothétie :

Tous les points du plan s'éloignent les uns des autres, proportionnellement au temps d'expansion.