Le pendule de Foucault Il nous donne la preuve que l'Univers dans son entier (actuel ou passé) agit dans notre environnement. Au pôle nord (ou sud) de la Terre, le plan du pendule reste fixe, par rapport à l'Univers entier. Faisant l'expérience, nous constatons qu'il semble pivoter en un jour sidéral, en 24 heures sidérales (vérifier)
Newton ou Einstein ?
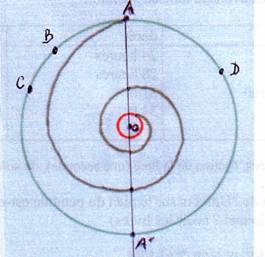
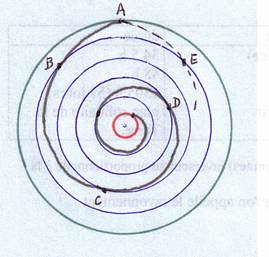
L'Univers dans sa globalité interagit sur notre environnement immédiat. Qu'apporte mon hypothèse géométrique à ce fait ? Nous avons vu comment la spirale V/V a une longueur voisine de celle du cercle. Au lieu de 2Õ, sa longueur est de Ö 4 Õ2 +1 Dans la première dimension, est-ce l'Univers actuel (cercle vert) qui interagit dans l'immédiateté sur le point A (Newton) ? Ainsi, sur la figure de gauche, les objets B, C, D, interagissent avec A, de façon inversement proportionnelle au carré de leur distance à A. Ou bien est-ce l'Univers passé, depuis l'origine (les deux spirales symétriques), qui interagit à la vitesse c (Einstein) ? Ainsi, sur la figure de droite, les objets B, C, D, E, tels qu'ils étaient dans le passé, interagissent aujourd'hui avec A, dans les mêmes conditions. Le résultat peut être le même dans les deux cas
Dans la deuxième dimension, même problème : est-ce la surface sphérique qui agit, ou la spiraloïde de révolution ? Qu'en est-il de la surface de la spiraloïde par rapport à celle de la sphère ? Etudier ce problème par la rotation de 360 degrés d'un demi-cercle autour de son diamètre, et la même rotation de la spirale autour d'un axe AO passant par le point théorique O autour duquel elle tourne. Il me semble que la surface engendrée par la rotation du demi-cercle (qui est la surface sphérique) est nettement plus grande que celle engendrée par la spirale, de même longueur. L'action gravitationnelle par la spiraloïde est-elle la même que celle de la sphère ? Dans ce cas, la différence des surfaces serait compensée par un éloignement différent.
Que dire pour la troisième dimension ? Noter que chaque fois que je parle de première, deuxième, troisième dimension, j'ajoute toujours le temps.
DERNIERES NOUVELLES Nous lisons dans la revue "Ciel et Espace" du mois d'août 2003 que le satellite WMAP vient de dresser le portrait le plus détaillé jamais obtenu de l'Univers. L'Univers a précisément 13,7 milliards d'années, à 200 millions d'années près. Autrement dit il a entre 13,5 et 14 milliards d'années. Dans mon travail, j'ai tablé sur 15 milliards d'années, chiffre communément admis ces dernières années. Cette différence ne modifie en rien mon hypothèse. Le satellite a permis également d'établir que la vitesse d'expansion de l'Univers est de 72 km/s par mégaparsec. Faisons le calcul :
Mégaparsec (Mpc) = 3,26 . 106 al Expansion : 72 km/s/Mpc, soit 0,022 m/s par année-lumière, soit 0,022.10-3 . km/s multiplié par 13,7.109 = 0,30.106 km/s = 3. 105 km/s soit 300 000 km/s pour la globalité de l'Univers. Conclusion, que je ne lis chez aucun auteur : l'Univers grandit, dans sa globalité, à la vitesse de la lumière
Ciel et Espace précise que "toutes les galaxies que les astronomes voient ne comptent que pour 4% de l'Univers" ! Dans mon hypothèse, sont exclus de l'observation ce qui est au delà de l'horizon tel que je l'ai défini, et ce qui est dans les zones aveugles. Egalement ce qui est caché par les poussières de notre Galaxie.
Retour sur le pendule de Foucault Suivant la latitude, nous pouvons constater que la durée de rotation du plan du pendule est de un jour multiplié par l'inverse du sinus de la latitude. Ainsi nos avons le tableau suivant :
Les marées, l'action de la lune (une seconde), du soleil (8 minutes) inversement proportionnelle à la distance. L'action de l'Univers sur le plan du pendule est-elle ce qu'on appelle le rayonnement gravitationnel ? (voir les livres)
|