Hubert Reeves énonce ainsi ce paradoxe: Deux jumeaux se trouvent sur une base de lancement de fusée. L'un reste au sol, l'autre entreprend un long voyage en capsule spatiale. Il atteint des vitesses voisines de celle de la lumière, fait le tour de Sirius et revient. D'après les horloges de la base, cent ans ont passé; Ses arrière-arrière petits enfants lui font une ovation. Lui a à peine changé : à son horloge de bord, trois mois se sont écoulés…
Voici une tentative d'explication géométrique.
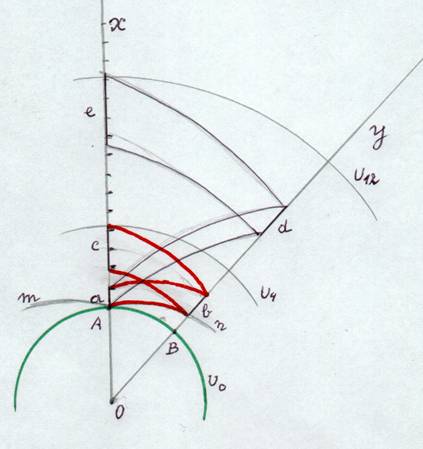
La lumière comme le voyageur suivent les géodésiques de l'espace-temps, soit les spirales que nous avons étudiées. Admettons que l'intervalle a est de un an Pour le sédentaire resté en A, le temps s'écoule régulièrement, suivant l'axe Ax, portant des graduations régulières, égales à a.. Pour le voyageur, le temps s'allonge au fur et à mesure de son déplacement, les années s'allongent sans qu'il s'en aperçoive. Les deux tracés noirs délimitent un intervalle de un an, qui grandit . Sur Oy, la durée d'un an est devenue d. Au retour sur Ax, ( l'Univers en expansion est devenu U12) la durée d'un an est devenue e. A son retour en A, moins d'années se sont écoulées pour lui depuis son départ, comparativement à ce qu'a vécu le sédentaire. UNE AUTRE EXPLICATION
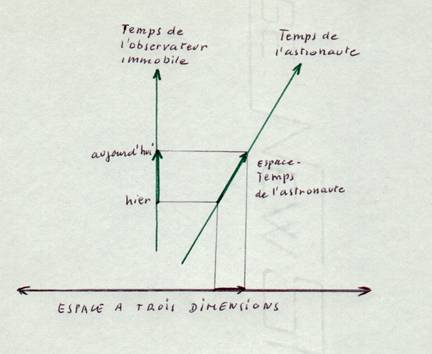
Voici une autre façon d'expliquer géométriquement le "paradoxe des jumeaux, tirée des livres des vulgarisateurs. En dehors des directions de l'espace, celle du temps prend des inclinaisons différentes, suivant le mouvement du mobile considéré. La figure montre des temps différents, suivant les vitesses. |