Les deux distances des galaxies

FICHE 13

Les arcs de spirale (en rouge) AB', B'C', C'D', sont égaux en longueur. Ils représentent le trajet de la lumière pendant l'unité de temps considérée (cette unité est figurée par l'intervalle entre les cercles).

Par contre, les arcs de cercle (en vert) correspondants AB, BC, CD ne sont pas égaux.

On a : AB < BC < CD .

Les arcs rouges sont les distances observées dans le passé, l'observateur étant en A. Les arcs verts sont les distances actuelles, inobservables.

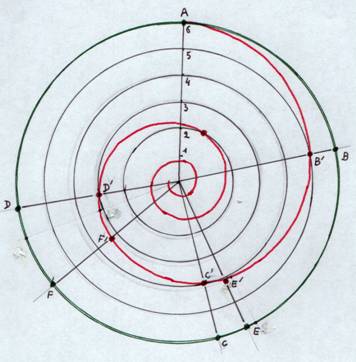
Dans son livre Le noir de la nuit, Edward Harrison écrit :

Si nous voulons, à l'aide de la relation vitesse-distance, comparer les vitesse de fuite des galaxies, nous devons utiliser leurs distances actuelles et non celles observées dans le passé lorsque ces galaxies avaient des éloignements différents. Ainsi la galaxie G', qui est à présent deux fois plus lointaine que la galaxie G, s'éloigne deux fois plus vite; mais la distance observée pour la galaxie G' n'est pas deux fois la distance observée pour la galaxie G.

C'est bien ce que montre la figure ci-dessus. On y voit que la galaxie E est actuellement, deux fois plus éloignée de A que la galaxie B (vert). Mais la distance observée pour E (AE') n'est pas deux fois la distance observée pour la galaxie B (AB' rouge).

Il faut donc distinguer la distance observée de la distance instantanée. Avec le problème que pose ce dernier mot en Relativité.

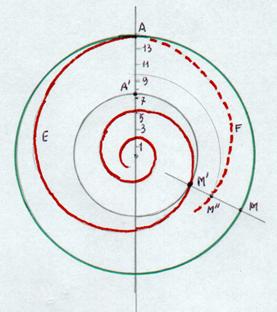
Longueur d'onde et décalage

Je cite encore Edward Harrison :

Supposons que la lumière reçue d'une galaxie lointaine ait ses longueurs d'onde multipliées par deux (soit un décalage égal à 1, correspondant à un accroissement de 100%). Les astronomes en déduisent immédiatement que l'Univers a doublé de taille depuis que la galaxie a émis cette lumière. La galaxie se trouve donc actuellement deux fois plus éloignée par rapport à sa position au moment de l'émission. Dans le même temps toutes les autres distances extragalactiques se sont multipliées par deux et le densité moyenne de l'Univers a été divisée par 8.

La situation décrite par Edward Harrison correspond, sur notre figure au verso, à la galaxie M.

La galaxie M se trouvait en M,' à 7,5 milliards d'années de l'âge de l'Univers.

Observons d'abord que le trajet de la lumière de M' en A, par la gauche de la figure, dépasse le demi-tour de l'Univers.

Cette galaxie M est visible dans la direction opposée, en M'', au dixième (environ) milliard d'années, c'est à dire plus tard.

Harrisson considère la distance instantanée de l'observateur en A', à la date 7,5, à la galaxie en M', et la compare à la distance instantanée actuelle, en M. Que l'on passe par la gauche ou par la droite, la distance a doublé.

Il existe un autre point ayant les propriétés de M, c'est son symétrique par rapport à l'axe (A). Dans la deuxième dimension de la surface sphérique, ce sera tout le cercle obtenu en faisant pivoter M' sur l'axe (A).Dans la troisième dimension, ce sera la surface sphérique centrée sur l'observateur A.

LA DISTANCE SEPARANT DEUX GALAXIES AUTRES QUE LA NOTRE

Les distances entre deux objets éloignés sont soumises à la géométrie courbe.

Comment concevoir la distance entre deux objets également éloignés de l'observateur, mais situés dans deux directions différentes ? Par exemple deux galaxies sont estimées à une même distance d de la nôtre, et sont vues par nous sous un angle de 60°.

Dans le plan d'Euclide, elles formeraient avec nous un triangle équilatéral et seraient distantes entre elles de d unités.

Sur la sphère tout change. Les trois angles ne sont plus égaux. Les trois côtés non plus, sauf s'il s'agit d'un triangle courbe, dont les trois côtés sont égaux à un quart de grand cercle, et les trois angles droits. Plus loin, la distance des deux galaxies diminue.

Le problème se complique si les galaxies sont vues sur la spiraloïde de révolution, dans le passé.