ANNEXE à la fiche 3         retour

Calcul de la trajectoire du mobile sur l'élastique en expansion

par Simon TRAPIER

L'élastique s'étire à une vitesse V.

Si sa longueur vaut 1 à l'instant t=0, elle vaudra à l'instant t:

La vitesse de chaque point de l'élastique est proportionnelle à son abscisse : ainsi, le point d'abscisse x a une vitesse :

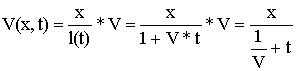
De plus, le mobile a une vitesse V par rapport à l'élastique : s'il se trouve à l'abscisse x, sa vitesse est donc :

C'est à dire :

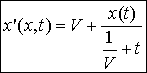
On obtient donc une équation différentielle dont la résolution donne :

où A est une constante dépendant de la position du mobile à t=0.

Ainsi, pour la courbe AA' , on a x(0)=0.

Donc :

et donc :

et l'équation de la trajectoire est finalement:

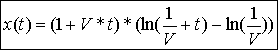
Cela permet ensuite de déterminer les coordonnées du point A', en résolvant l'équation:

Ce qui donne :  et  avec  e =2.71…

Et de la même manière, on détermine les équations de BB', CC', DD', et les coordonnées de B', C' et D', en changeant simplement la valeur de la constante A dans l'équation de x(t).